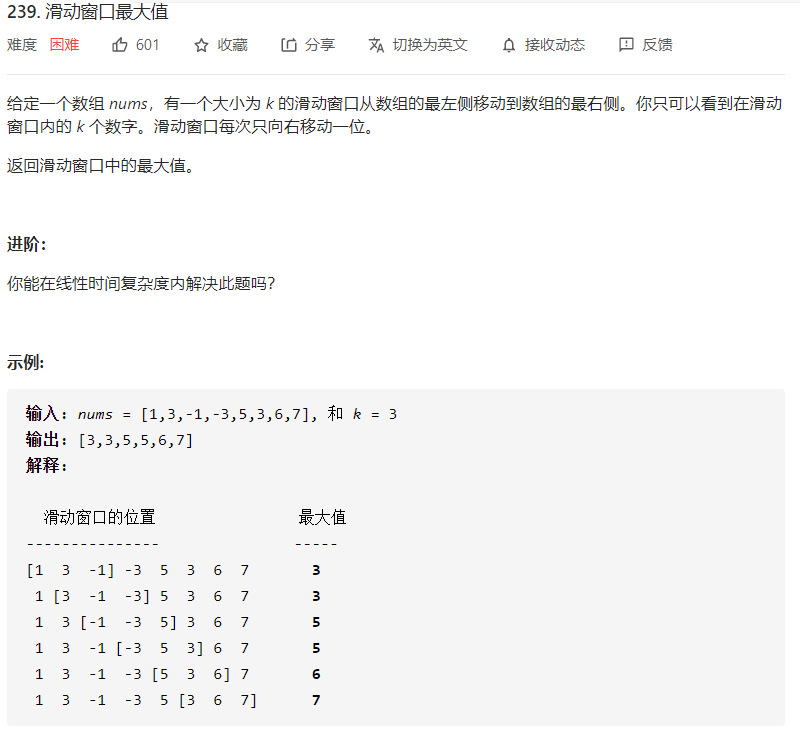
题目分析
这个问题也是经典的算法之一了,也是图像处理或者信号处理中常常需要处理的问题。解法并不困难,能否找到最好的求解方法是这个题目的关键,小伙伴们先想一想如何解答。在两年前做过本题,今天又遇到他了,补充一下java的题解和使用堆的做法。
暴力法
暴力法不需要过多解释,代码也非常简单。把每一个区间都遍历一下,求出最大值即可,但是对于本题来说,数据量较大会超时。
算法的**时间复杂度为$O(nk)$,空间复杂度为$O(n)$**。
1 | class Solution(object): |
大顶堆
大顶堆的解法也很容易理解,每次从堆中移走一个元素,并且将一个新的元素放入堆中,并且取出堆顶元素表示滑动窗口中的最大元素。
要从堆中找到最大的元素,因此算法的**时间复杂度为$O(nk)$,空间复杂度为$O(n)$**。
1 | class Solution { |
优化大顶堆
提交堆的写法后,发现还是TLE了。我们想一下是否可以优化堆的写法,为什么会超时间呢?我们发现向堆中插入元素的时间复杂度是O(log(n)),但是删除任意一个元素的时间复杂度是O(n)。
因此我们尽量不要寻找某一个元素,而是想一想是否可以只删除影响堆顶的元素呢?
算法的**时间复杂度为$O(nlogk)$,空间复杂度为$O(n)$**。
1 | class Solution { |
单调队列
思考这个问题,滑动窗口出现一个很大的数字M时,那么滑动窗口中小于等于该数字的都是无意义的,因为如果取得这些数,一定不如取M。因此我们需要维护一个单调递减的队列。
要注意和单调栈的区别,单调递减的栈中,最大元素是永远不会被弹出的,而滑动窗口中的最大元素可能会弹出。因此我们在滑动窗口中保存元素的索引位置,当第一个元素的索引已经不在窗口中时,将该元素弹出。
算法的**时间复杂度为$O(n)$,空间复杂度为$O(n)$**。
1 | from collections import deque |
在上面的写法中,我们往队列中add的是元素的索引,我们能否add元素值呢?答案也是可以的,因为队列是单调递减的。因此如果窗口的左边等于队列头,则说明需要将队头移除。
并且插入元素时要保证队列单调递减,因此要将队尾小于该元素的值都移除。注意此时等号是不可以取到的。因为等号取到可能会把前面相等的最大值都给移除掉,这样下次移除的最大值就不是最左端的元素,而是刚刚加入的元素。
1 | class Solution { |
刷题总结
小伙伴们遇到这个题目,一定不要用暴力法求解,一旦用了,基本上是挂了。现在招聘的难度越来越大,内卷越来越严重。因此算法题基本上都是力扣mid以上,所以小伙伴们要多刷mid和hard题,提高自身的实力。